How To Tell If A System Of Equations Has No Solution Or Infinitely Many
How to tell if a system of equations has no solution or infinitely many. If the b is in the column space of A and since det A0 then it will have infinitely many solutions. In the linear equation given below say whether the equation has exactly one solution or infinitely many solution or no solution. If the rank of both matrices is equal but if the rank is lesser than the number of unknowns then the system of equations is consistent and has infinitely many solutions.
Here is a problem that has an infinite number of solutions. X y 10 2 x 2 y 20 x y 10 2 x 2 y 20 Thats consistent because the solutions are the line x y 10 x y 10. 3x2y 12 -6x-4y24 If you solve this your answer would be 00 this means the problem has an infinite number of solutions.
There are two cases actually. A system of linear equations is two or more linear equations that have the same variables. A system of linear equations usually has a single solution but sometimes it can have no solution parallel lines or infinite solutions same line.
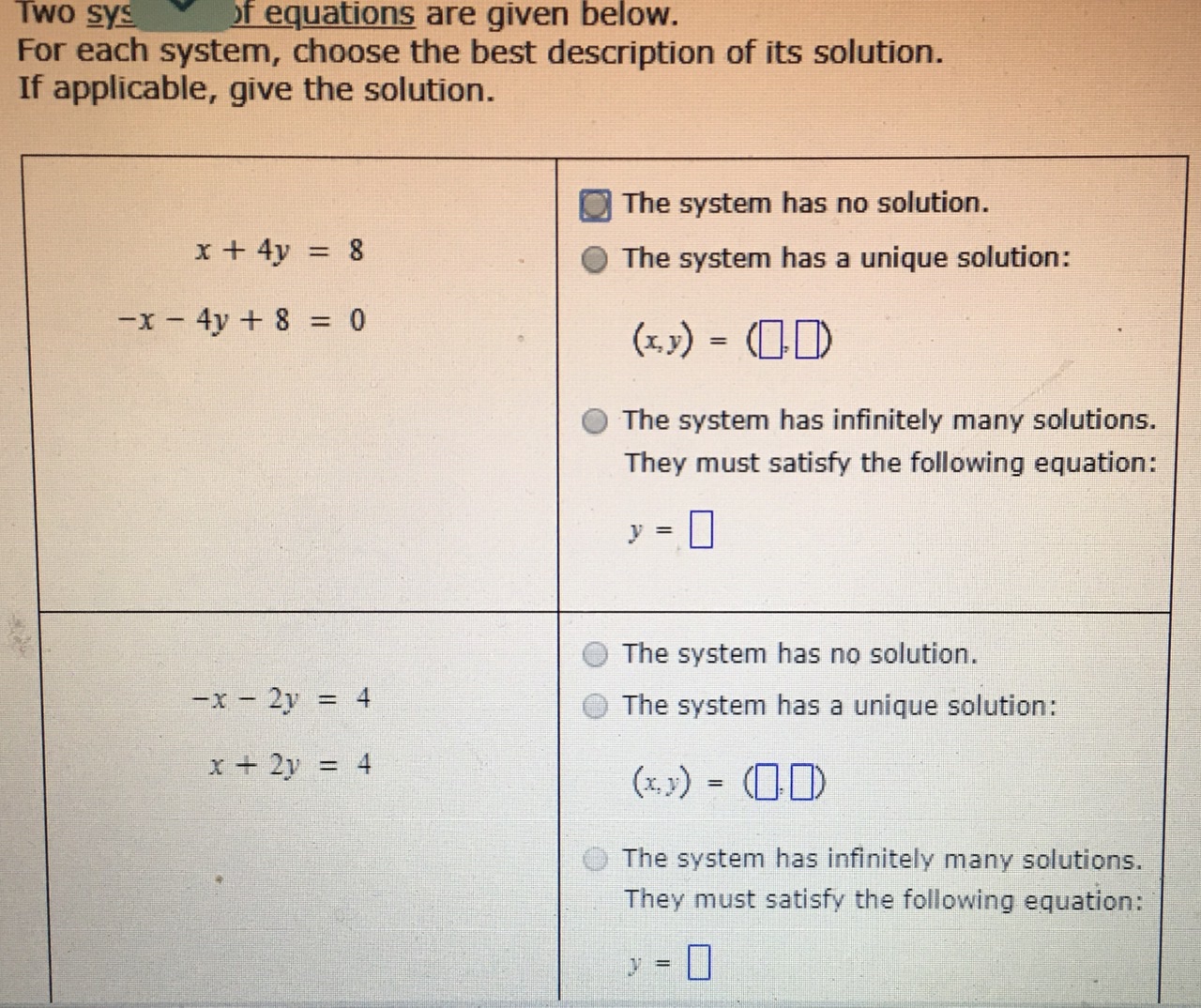
In order to find if they have no solution or infinite solutions you need to find the y-intercepts of both lines. They must satisfy the following equation. This article reviews all three cases.
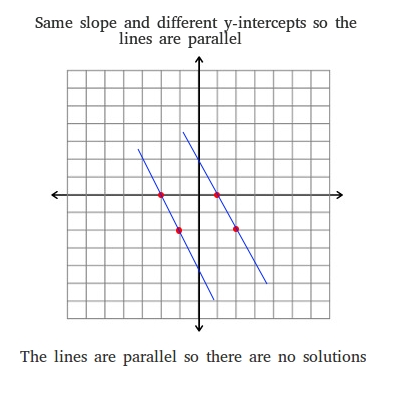
If solving it leads to a contradiction eg10 it has no solutions. So this system of equations has no solution. It is impossible for the equation to be true no matter what value we assign to the variable.
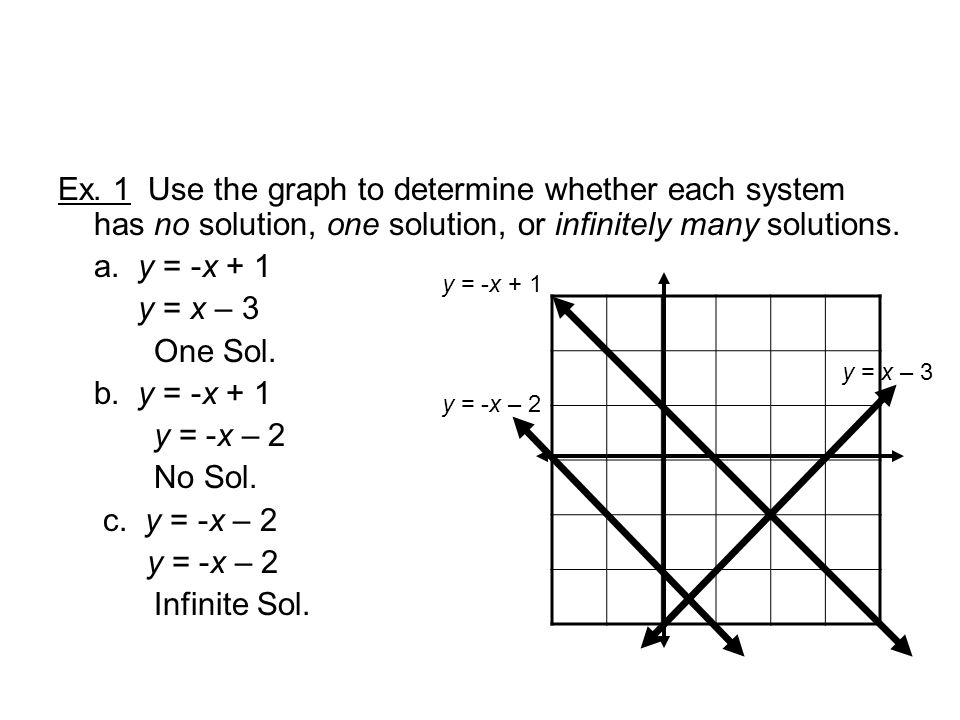
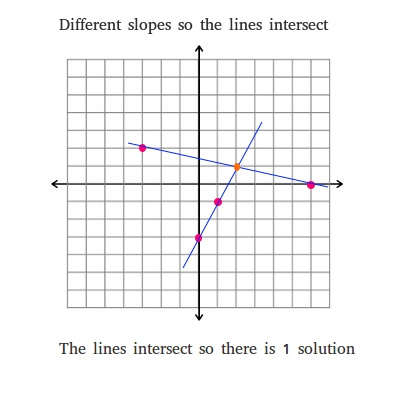
If it lead to something like. You can graph the equations as a system to find out whether the system has no solutions represented by parallel lines one solution represented by intersecting lines or an infinite number of solutions represented by two superimposed lines. So subtract 4x on both sides to get rid of x-terms.
For an answer to have no solution both answers would not equal each other. For an answer to have an infinite solution the two equations when you solve will equal 00.
Y the answer is the system has infinitely many solutions.
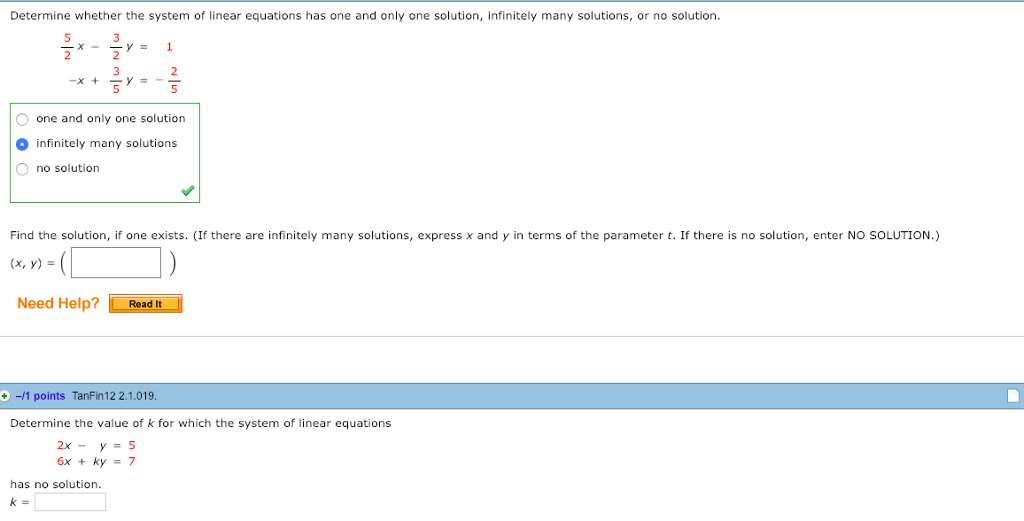
Therefore this system of linear equations has no solution. A system of linear equations usually has a single solution but sometimes it can have no solution parallel lines or infinite solutions same line. Alternatively you can plug a set of numbers into the equations to see if you get the same outcome for both equations. If solving it leads to a contradiction eg10 it has no solutions. When we solve the given equation we dont find x in the result. C Infinitely many solutions D None of these. If the vector b is not in the column space of the matrix A it will have no solutions. -x2y-2 x-2y2 the system has no solution the system has a unique solution. How do you tell if a system of equations has no solution or infinitely many.
3x2y 12 -6x-4y24 If you solve this your answer would be 00 this means the problem has an infinite number of solutions. For example 2x3y10 2x3y12 has no solution. How do you tell if a system of equations has no solution or infinitely many. The constants are the numbers alone with no variables. You can graph the equations as a system to find out whether the system has no solutions represented by parallel lines one solution represented by intersecting lines or an infinite number of solutions represented by two superimposed lines. If a system of equations has no solutions then it is inconsistent. 4x 2 4x - 5.

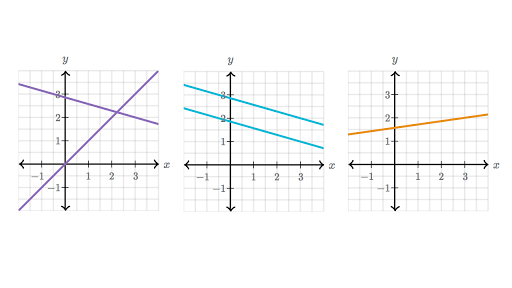


































Post a Comment for "How To Tell If A System Of Equations Has No Solution Or Infinitely Many"